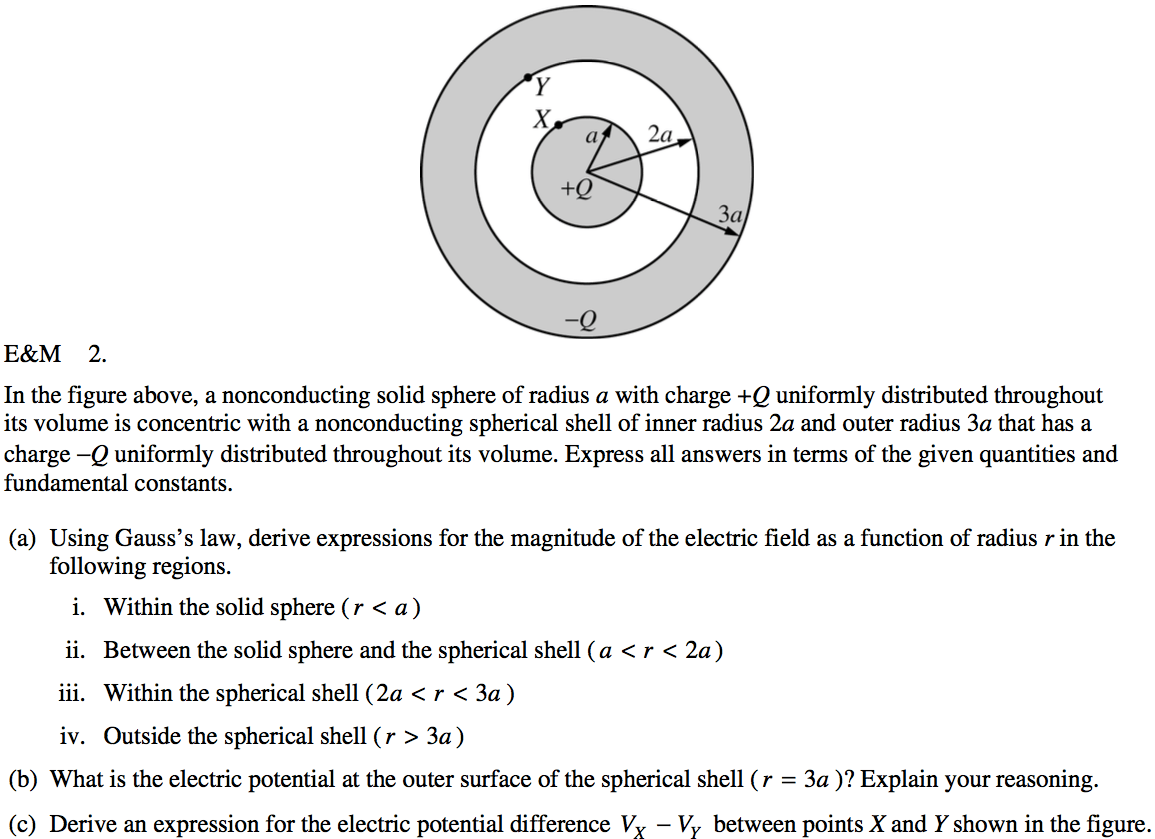
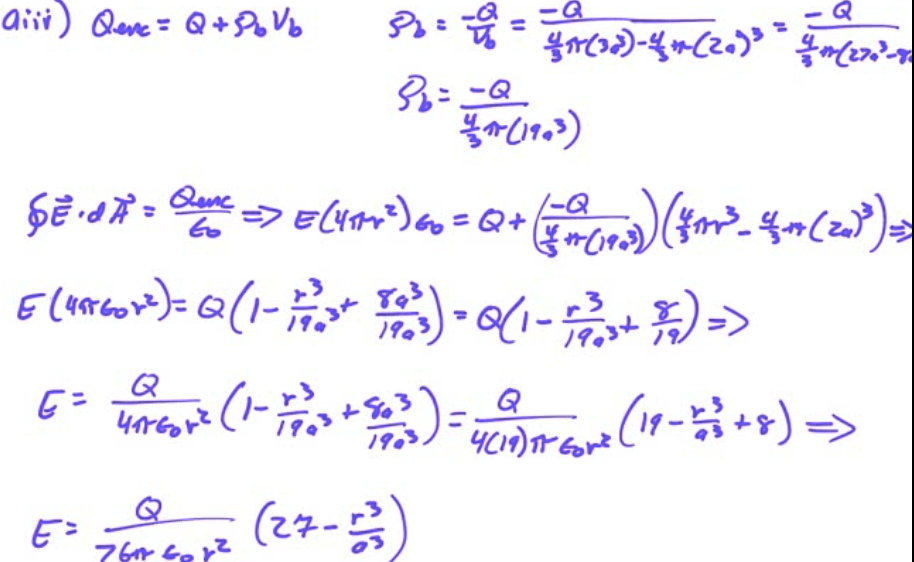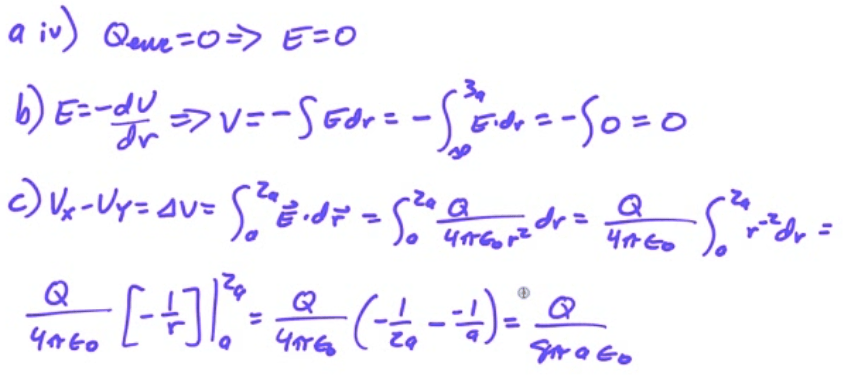Potential Due to a Charged Ring
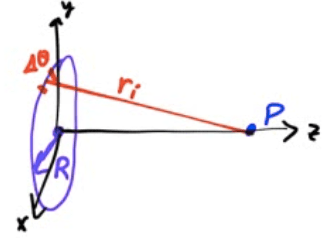
Find the electric potential on the axis of a uniformly charged ring of radius R and total charge Q at point P located a distance z from the center of the ring
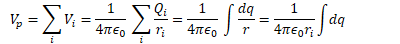
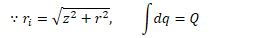
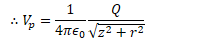
Potential Due to a Charged Disk
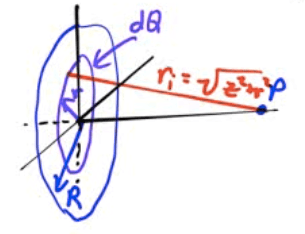
Find the electric potential on the axis of a uniformly charged disk of radius R and total charge Q at point P located a distance z from the center of the ring
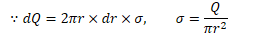

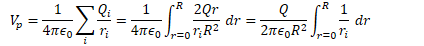
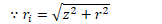

Potential Due to a Spherical Shell of Charge
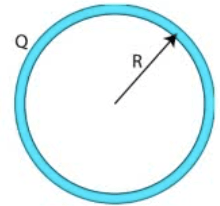
Find the electric potential both inside and outside a uniformly charged shell of radius R and total charge Q

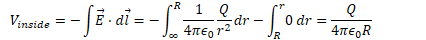

Potential Due to a Uniform Solid Sphere
Find the electric field and electric potential inside a uniformly charged solid insulating sphere of radius R and total charge Q
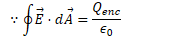
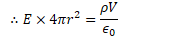
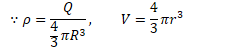
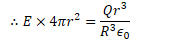
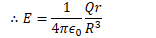
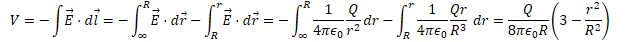
2012 Free Response Question 1
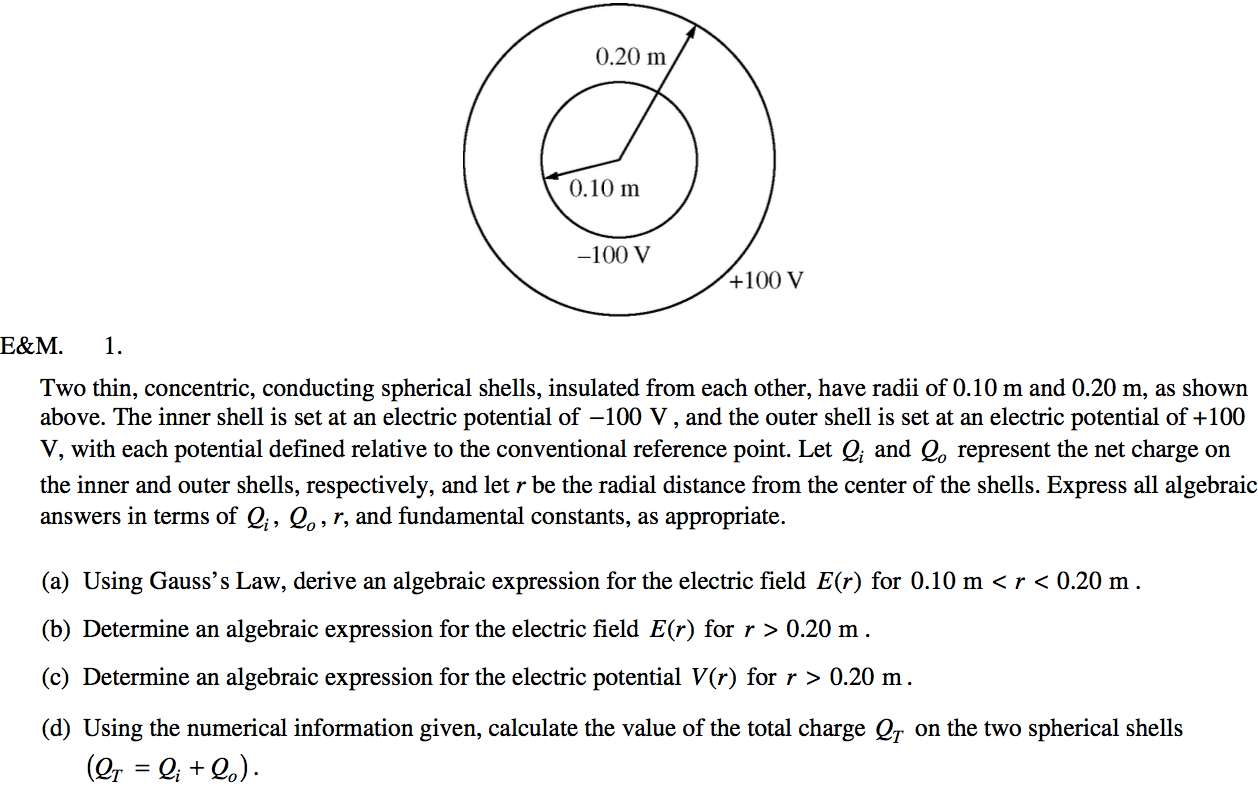


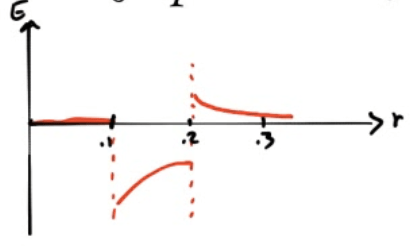
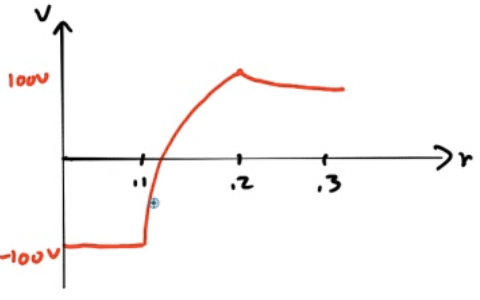
2010 Free Response Question 1
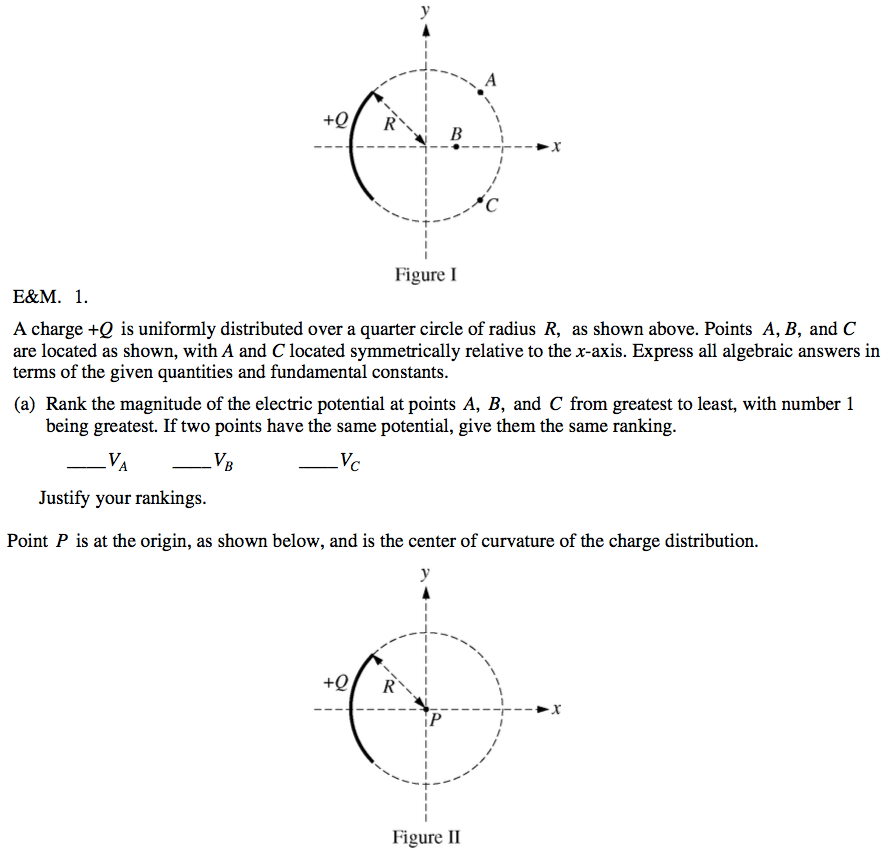
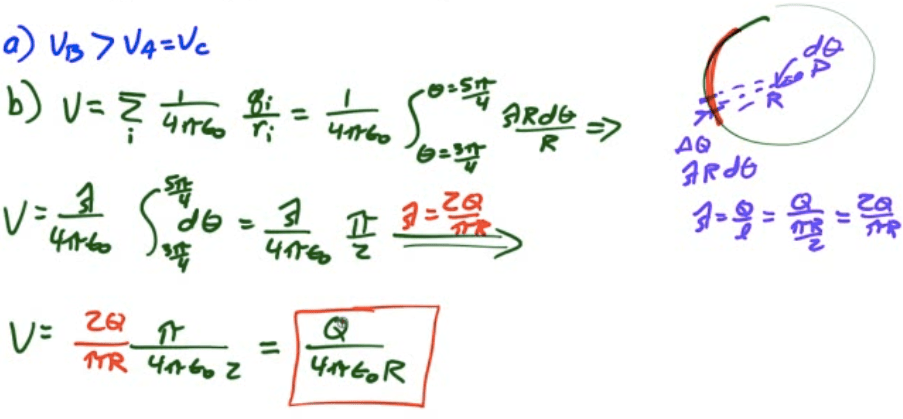

2009 Free Response Question 1




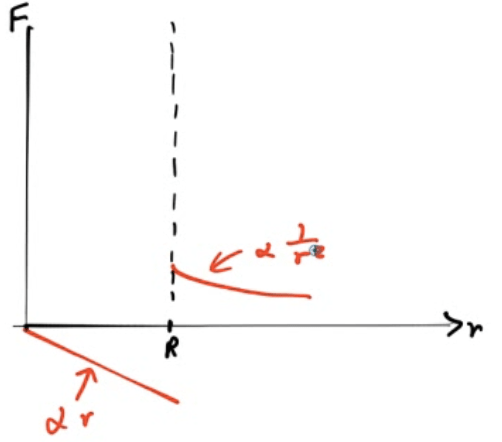
2007 Free Response Question 2