Question 4
Eddy current brake

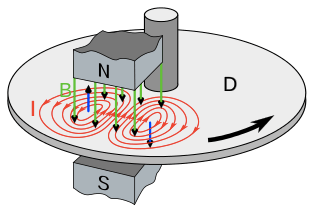
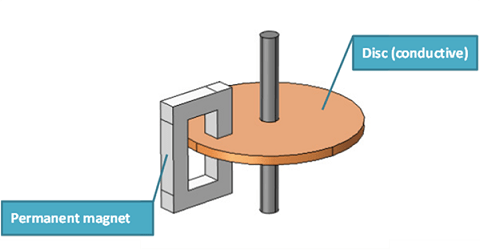
Eddy

Question 9
Magnetic Field due to a Current Loop

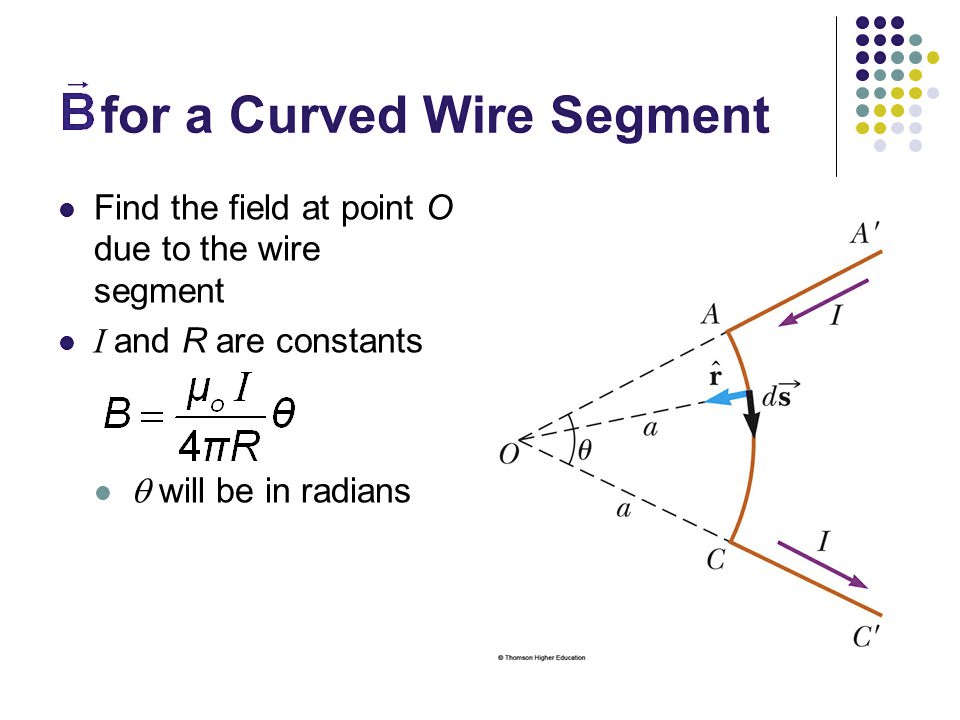

Question 10
Energy in a capacitor

Question 21

Question 22

Formula for inductance of simple solenoids

Derivation


Question 23


Question 28

Question 29

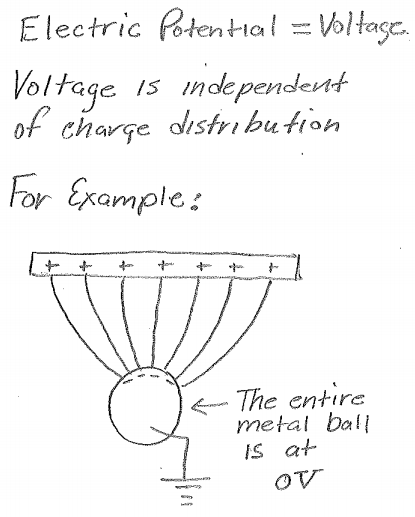

Question 30
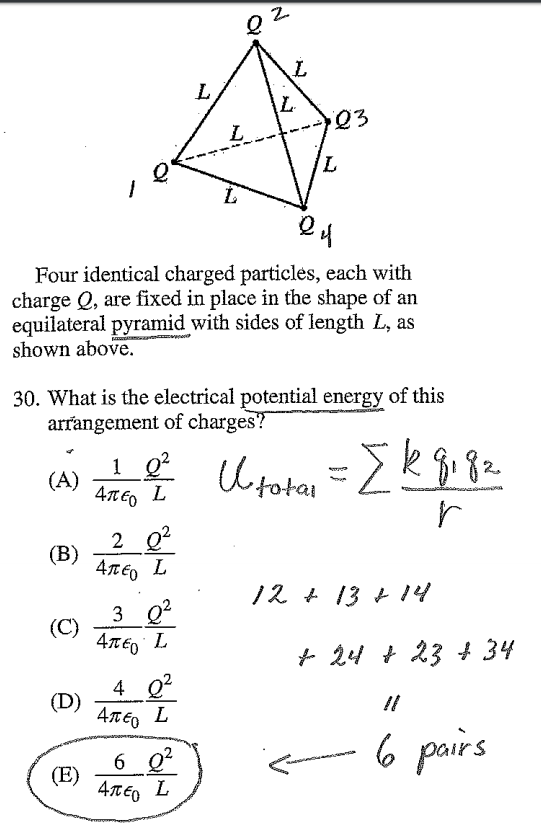
Question 31
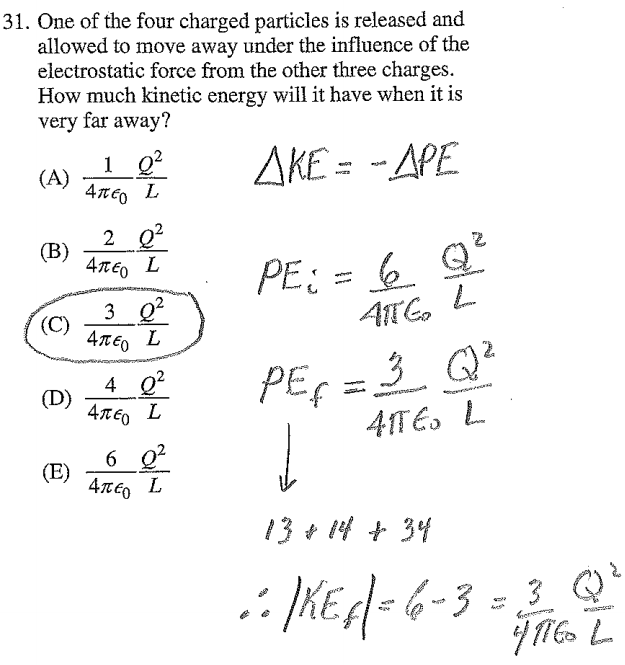
Question 33
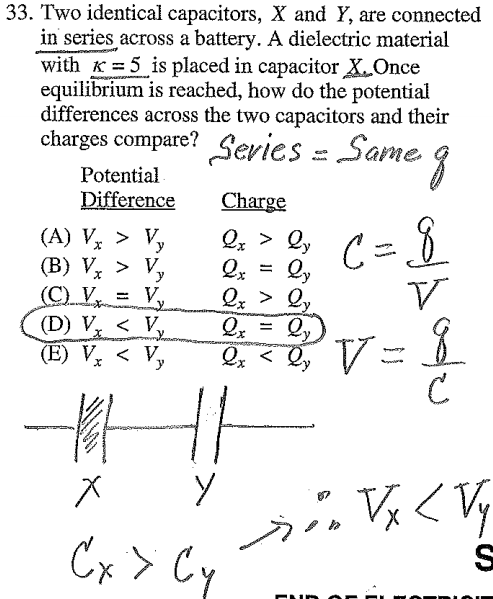
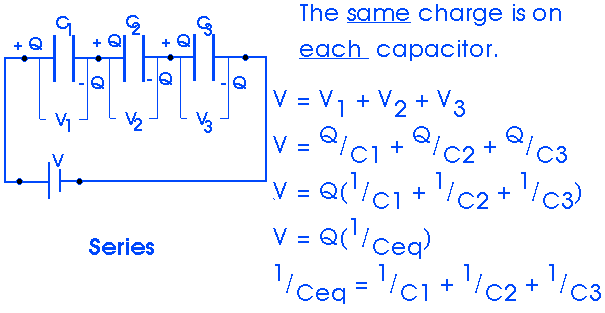
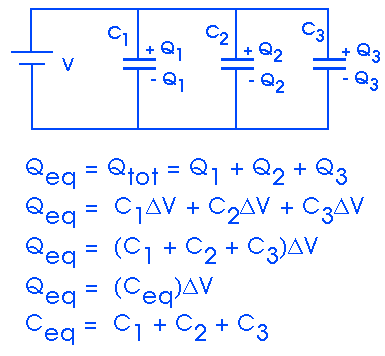
Question 35
