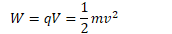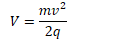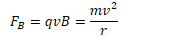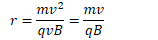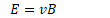Magnetic Fields
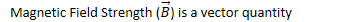
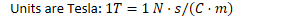
1 Tesla is a very strong magnetic field
More common non-SI units is the Gauss
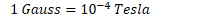
Earth's magnetic field strength ≈ 0.5 Gauss
Forces on Moving Charges
The magnetic force is always perpendicular to the charged object's velocity, therefore the magnetic force on a moving charge is never applied in the direction of the displacement, therefore a magnetic force can do no work on a moving charge (but it can change its direction)
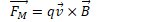

Direction of the Magnetic Force
Direction of the force given by right-hand rule
Point fingers of right hand in direction of positive particles' velocity
Curl fingers inward in the direction of the magnetic field
Thumb points in the direction of the force on charged particle

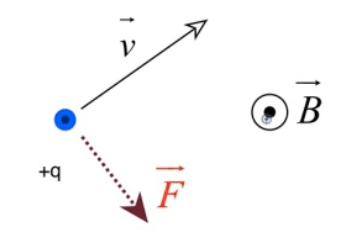
Path of Charged Particles in B Fields
Magnetic force cannot perform work on a moving charge
Magnetic force can change its direction (moving it in a circle if the magnetic force is constant)
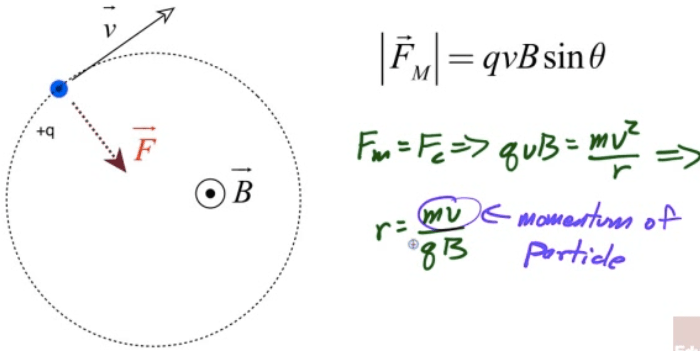
Total Force on a Moving Charged Particle
E field can do work on a moving charge
B filed can never do work on a moving charge
Lorentz Force
Velocity Selector
A charged particle in crossed E and B fields can undergo constant velocity motion is v, B, and E are all selected perpendicular to each other
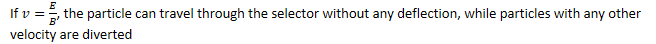
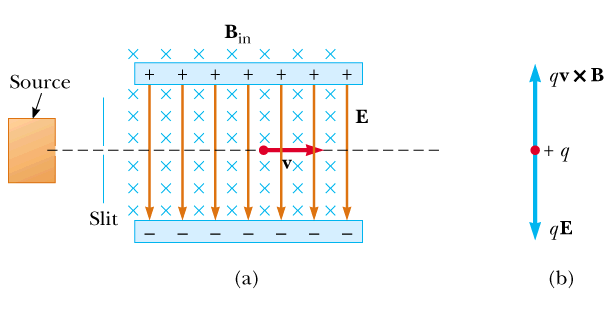
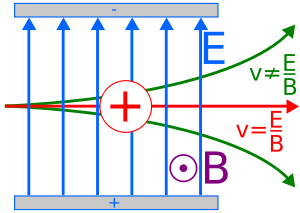
Mass Spectrometer
Magnetic fields accelerate moving charges so that they travel in a circle
This can be used to determine the mass of an unknown particle!
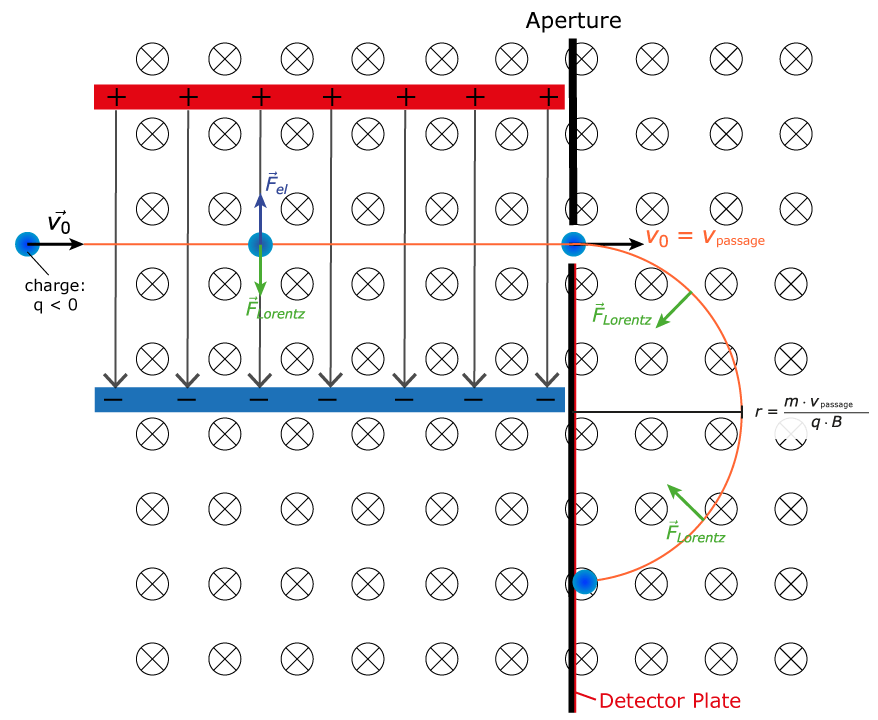
Example 1: Velocity Selector
Find the speed of a charged particle which passes through a velocity selector with magnetic field strength of 1 Tesla perpendicular to an electric field of 600,000 N/C
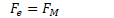
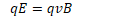

Example 2: Mass Spectrometer
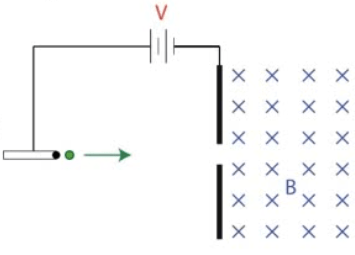
- A proton is accelerated through a potential difference V before passing into a region of uniform magnetic field B as shown
Determine the voltage necessary to give the proton a speed v as it enters the magnetic field region in terms of the proton's mass m, its velocity v, and its charge,
q.Determine an expression for the radius of the proton's motion in the uniform magnetic field
region
Sketch the path of the proton in the magnetic field
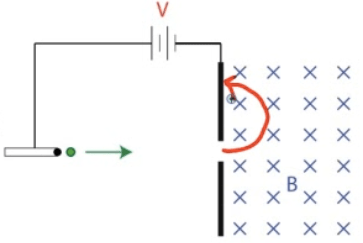
An electric field is applied in the same region as the uniform magnetic field. Determine the magnitude and direction of electric field required so that the proton passes through the region in a straight line