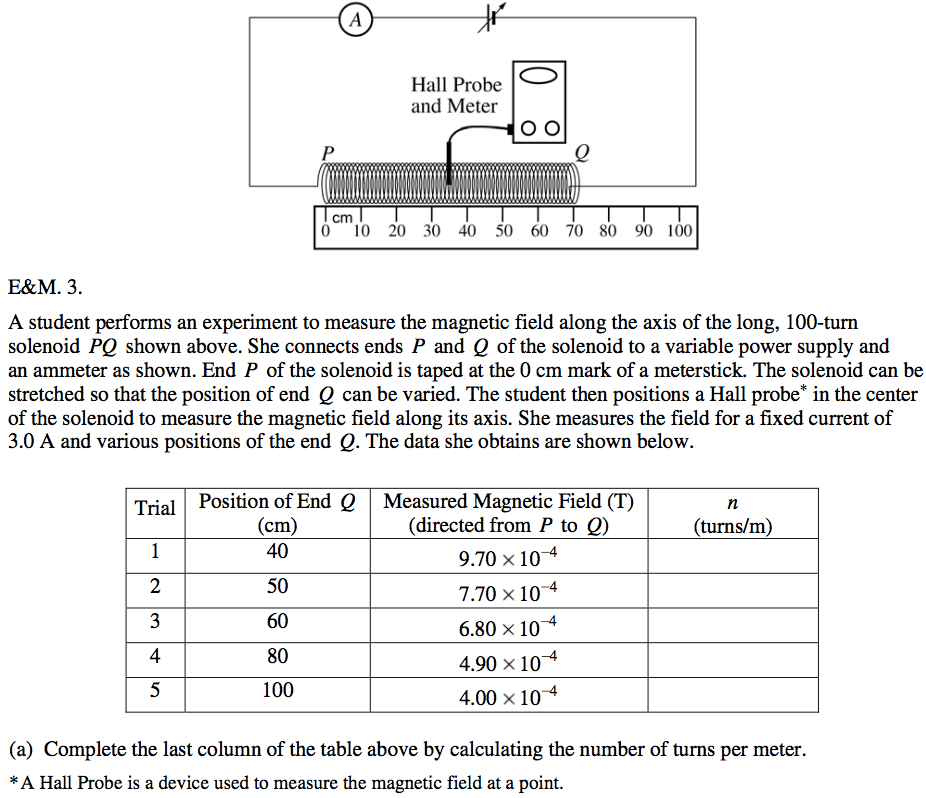
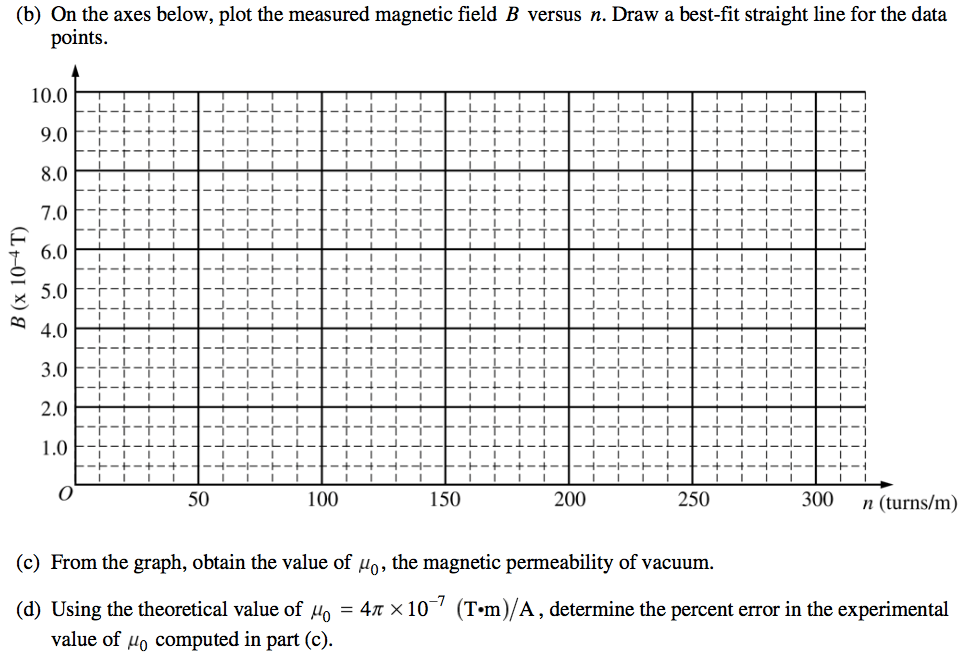
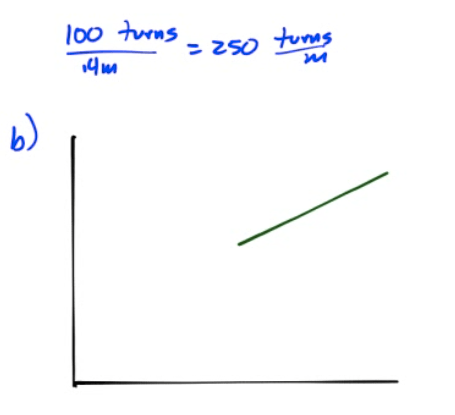
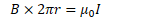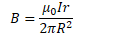Ampere's Law
Ampere's Law provides an elegant method of finding the magnetic field due to current flowing in a wire in situations of planar and cylindrical symmetry
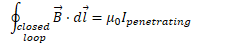
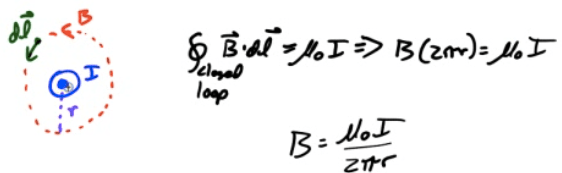
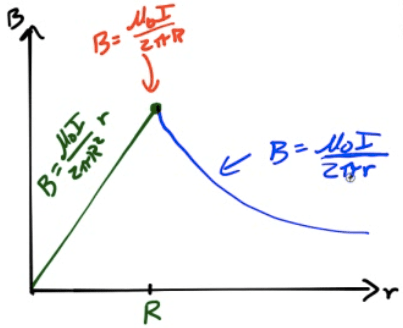
Example 1: Magnetic Field of a Wire
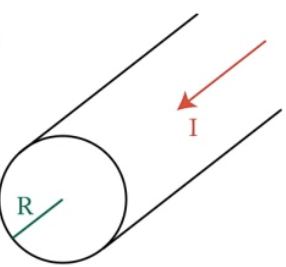
- Find the magnetic field outside a current-carrying wire
- Find the magnetic field inside a current-carrying wire
Graph the magnetic field of a current-carrying wire as a function of the distance from the center of the wire
Example 2: Magnetic Field in a Solenoid
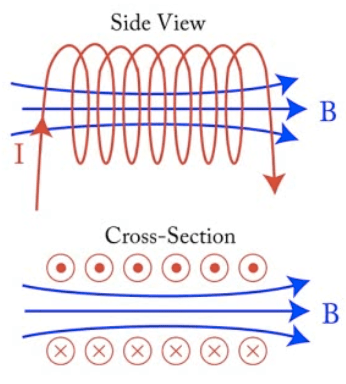
Calculate the magnetic field in the middle of a solenoid (i.e. Slinky) using Ampere's Law
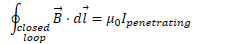
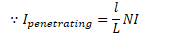
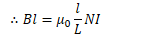
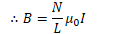
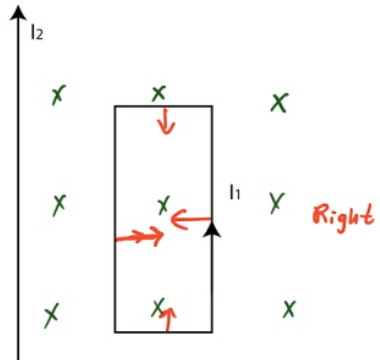
Example 3: Net Force on a Wire Loop

What is the direction of the net force on the loop?
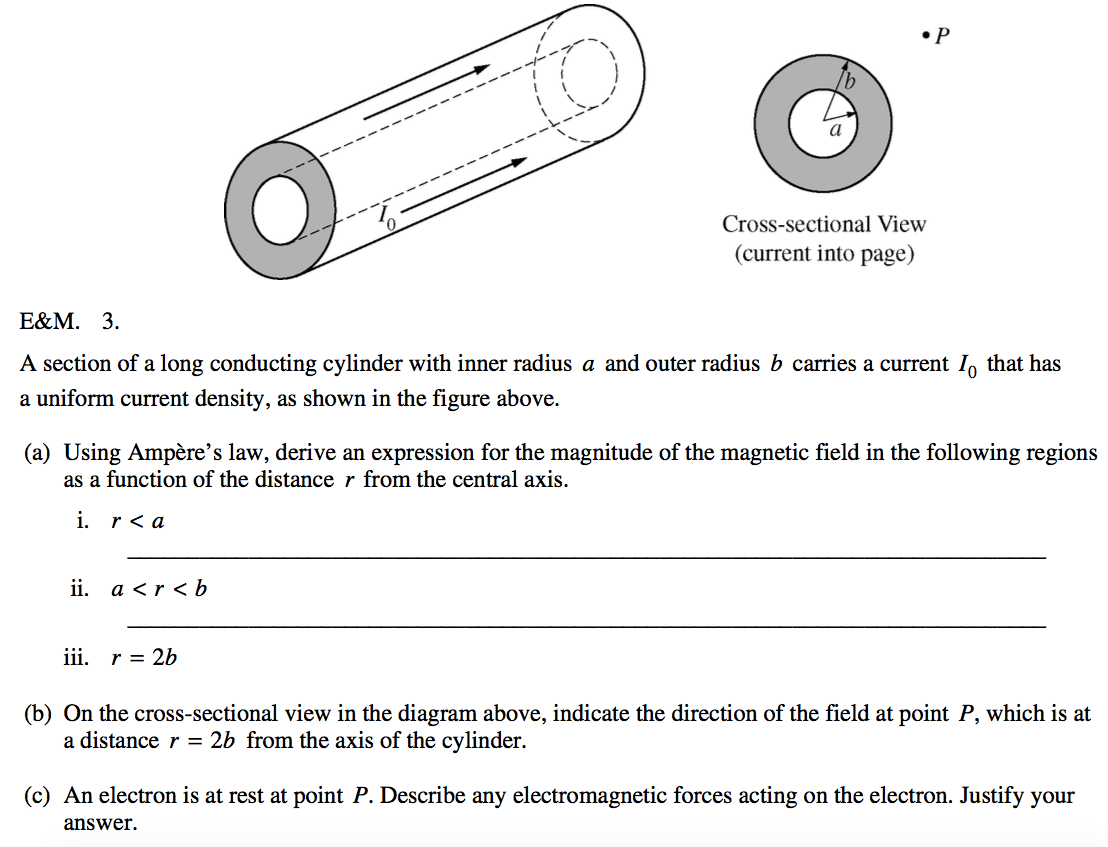
2011 Free Response Question 3

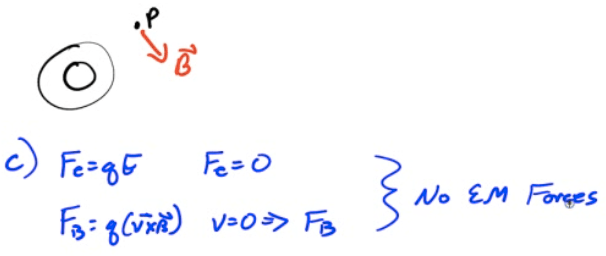
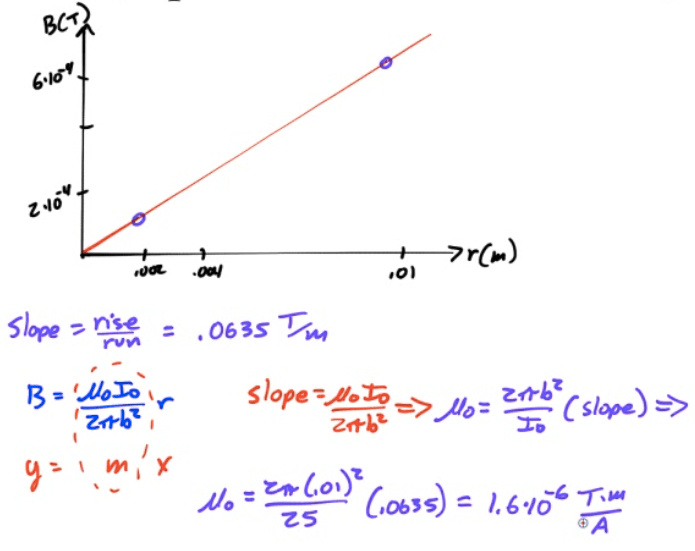
2005 Free Response Question 3