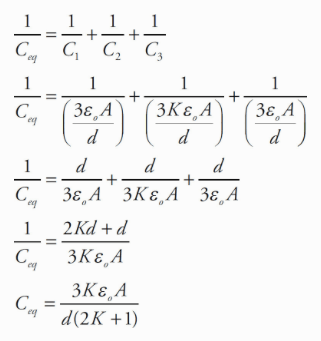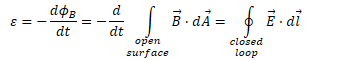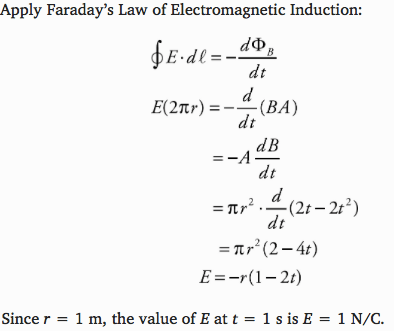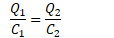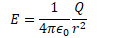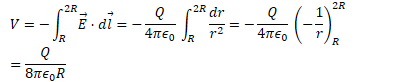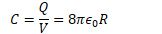Question 41
N=m·kg·s-2
J=m2·kg·s-2
C=A·s
V=m2·kg·s-3A-1
T=kg·s-2A-1
Question 48
Question 53
Parallel
capacitors:
Question 56
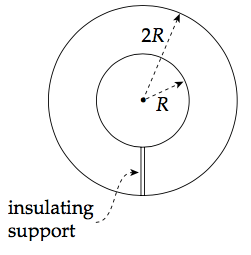
Calculating Capacitance
Assume a charge of +Q and -Q on each conductor
Find the electric field between the conductors (Gauss's Law)

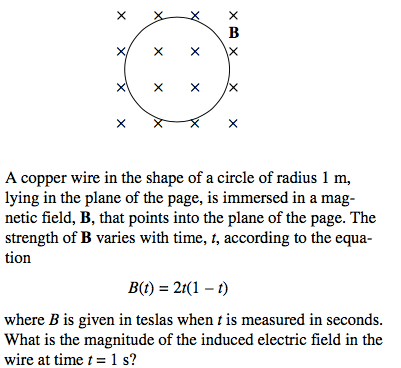
Question 57
Since the magnetic force is always perpendicular to the object’s velocity, it does zero work on any charged particle.
Zero work means zero change in kinetic energy, so the speed remains the same.
Remember: The magnetic force can only change the direction of a charged particle’s velocity, not its speed.
Question 61
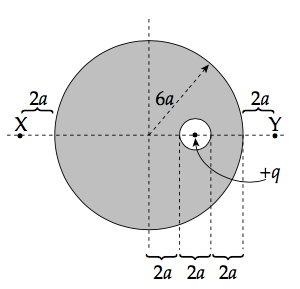

Question 66